Borda Count Method: Basics and an Example
Borda Count Method: this article provides a practical explanation of the Borda Count Method. Next to what it is, this article highlights a concrete calculation example and the solution, the critism and the alternatives. After reading, you’ll understand the basics of this powerful decision-making tool. Enjoy reading!
What is the Borda Count Method? The basics explained
The Borda Count Method is a simple tool that is used in elections and decision-making in various contemporary situations. Each candidate is given a number of points, and once all votes have been counted, the option with the most points awarded is considered the best, and therefore the winner of an election, competition or other decision.
The Borda Count Method is intended to be able to choose different options and candidates, rather than the option that is preferred by the majority. For this reason, it is also described as a consensus-based voting system. The opposite of this is a majority system.
Because of this consensus behavior, the Borda Count Method is commonly used in awarding sports awards, for example to determine the Most Valuable Player in baseball, to rank teams in NCAA sports, and to award the Heisman trophy.
The Borda Count Method has been developed in many different time periods, each time independent of the previous period. For instance, the calculation tool was first developed by Ramon Lulll in the thirteenth century.
However, it was the French mathematician and marine engineer Jean-Charles de Borda after whom the tool was named.
He devised the system in 1770. Nowadays, the system is still being used as a voting system to elect members of parliament in Nauru. The Borda Count Method is also actively used within the parliamentary democratic republic of Slovenia. Outside parliament settings, the tool is also used by various organisations and competition organisers worldwide.
Borda Count Method example including the calculation and solution
In the Borda Count Method, points are given to each choice based on ranking. For example, the lowest rank gets 1 point, and each consecutive spot on the list gets an extra point. If there are four options, the top rank is therefore awarded with 4 points. Mathematically, the first rank gets N points, the second N-1, the third N-2, and the fourth N-3, etc.
Here’s a calculation example. A group of 100 astrophysicists comes together for an annual conference. They live across the European continent, close to the cities Budapest, Amsterdam, Oslo, and Seville. To determine where the conference will be held, they decide to use the Borda Count Method to vote on the most suitable location.
The results of the vote are shown in the table below.
Figure 1 – Borda Count Method example
The 100 ballots are collected, and counting commences. In the table above, we see that 53 ballots have Amsterdam as the preferred city. Amsterdam therefore receives N points (4). Amsterdam is followed by Oslo (N-1), Budapest (N-2) and Seville (N-3).
If the rules explained above are applied to all ballots, the result is an overview with the amount of points per option.
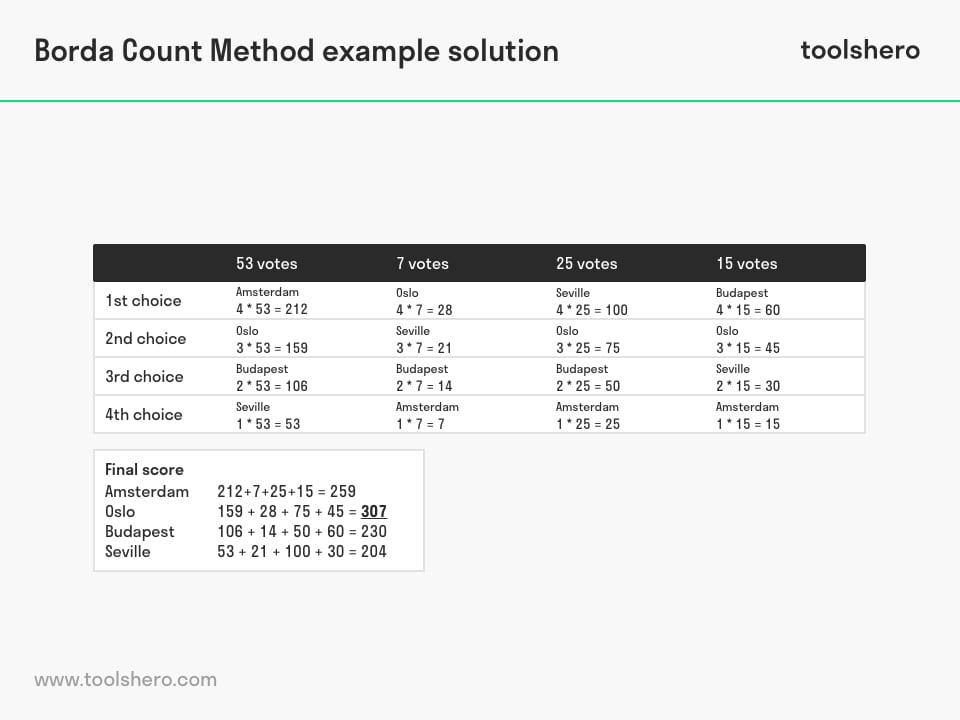
Figure 2 – Borda Count Method example solution
If all points are added up, the final score is as follows:
Amsterdam: 212 + 7 + 25 + 15 = 259
Oslo: 159 + 28 + 75 + 45 = 307
Budapest: 106 + 14 + 50 + 60 = 230
Seville: 53 + 21 + 100 + 30 = 204
Assuming the Borda Count Method is decisive for the choice of city, Oslo is the winner in this vote.
Criticism of the Borda Count Method
In the example above, Amsterdam has the majority of first choice votes, yet Oslo is the winner. Therefore, the Borda count violates the majority criterion, going directly against the principle that the will of the majority is decisive.
Although 51 percent of the astrophysicists indicated Amsterdam as their preferred city, Oslo came first in the calculations. This is due to compromises.
The Borda Count Method is a consensus-based voting system. In the example, Oslo is the location for which the hundred scientists have to make the least concessions. Compromises, however, open the door to manipulation and tactical voting.
Manipulation
Voters can influence the outcome by insincerely impairing the position of the first-choice candidate compared to the second-choice candidate. They may also help a preferred candidate by impairing the position of the second-choice candidate on the ballot.
For this reason, the French Academy of Sciences (of which Borda was a member) abandoned the system. One reason for this is that they discovered that other people knew how to manipulate the Borda rule.
These people were able to place their rivals at the bottom of the list, thus directly eliminating many candidates. In response to this point of criticism, the inventor of the system said: ‘My system is only intended for honest men’.
Borda Count Method alternatives
Plurality System
This is also referred to as ‘the winner takes all’ system. In this system, the top ranking is simply awarded to the person with the most votes. The candidate doesn’t have to have more than 50 per cent of the votes, but only needs to have more votes than the other candidates.
Compared to the Borda Count Method, these kinds of plurality systems however do not represent the interests of most voters. The plurality system is very common in American politics.
Majority System
In this electoral system, an attempt is made to offer a high degree of representativeness by requiring candidates to get a majority of votes. Majority support here means more than 50 per cent. If no candidate succeeds in achieving this, a second round is organised.
During this second round, only limited participants from the first round may participate. There are different variations on this system. In Russia, for example, the two largest candidates move on to the second round. In France, all candidates with a minimum percentage of 12,5 participate in the second round.
To Summarise
In the thirteenth century, Jean-Charles de Borda devised a method for facilitating voting procedures in politics. In this system, points are given to multiple options. The option with the most first-choice votes gets N points.
Every subsequent option receives 1 less point. Eventually the points are added up for each option, and the option with the most points wins the vote.
This means that even the option with more than 50 per cent of all preferred votes may not end up in first place. For this exact reason, the organisation behind the method—the French Academy of Science—decided to abandon the method.
Other broadly acceptable options and common voting systems are the plurality and majority systems. These are less susceptible to manipulation.
Now It’s Your Turn
What do you think? Are you familiar with the explanation of the Borda Count Method? Are there situations in which you could use this voting Borda tool yourself? What other voting systems do you know? Which of these systems is the least susceptible to manipulation and fraud? Do you have any tips or additional comments?
Share your experience and knowledge in the comments box below.
More information
- Black, D. (1976). Partial justification of the Borda count. Public Choice, 28(1), 1-15.
- Lansdowne, Z. F., & Woodward, B. S. (1996). Applying the borda ranking method. Air Force Journal of Logistics, 20(2), 27-29.
- Lumini, A., & Nanni, L. (2006). Detector of image orientation based on Borda Count. Pattern Recognition Letters, 27(3), 180-186.
- Ratliff, T. C. (2002). A comparison of Dodgson’s method and the Borda count. Economic Theory, 20(2), 357-372.
How to cite this article:
Janse, B. (2019). Borda Count Method. Retrieved [insert date] from Toolshero: https://www.toolshero.com/decision-making/borda-count-method/
Original publication date: 09/09/2019 | Last update: 03/25/2024
Add a link to this page on your website:
<a href=”https://www.toolshero.com/decision-making/borda-count-method/”>Toolshero: Borda Count Method</a>
Ben Janse
Ben Janse is a young professional working at ToolsHero as Content Manager. He is also an International Business student at Rotterdam Business School where he focusses on analyzing and developing management models. Thanks to his theoretical and practical knowledge, he knows how to distinguish main- and side issues and to make the essence of each article clearly visible.
Related ARTICLES
Stakeholder Analysis explained plus template
Prospect Theory by Amos Tversky and Daniel Kahneman
Convergent Thinking: the Definition and Theory
Decision Making Unit (DMU) explained
Decision Matrix Analysis
