Paired Comparison Method plus example
Paired Comparison Method: this article explains the Paired Comparison Method in a practical way. Besides what it is, this article also highlights the six basic steps and a worked real-world example. After reading you will understand the basics of this decision-making method. Enjoy reading!
What is the Paired Comparison Method?
Paired Comparison Method is a handy tool for decision making; it describes values and compares them to each other.
It’s often difficult to choose the best option when you have different ones that are far apart.
All the potential options are compared visually, leading to an overview that immediately shows the right decision. This makes it possible to compare the relative importance of opposing criteria in a simple way.
If there is no objective data available for making the decision, Paired Comparison Method can be a very handy tool. This method is also known as the Paired Comparison Method and Pairwise Comparison.
Priorities
Paired Comparison Method can be used in different situations. For example, when it’s unclear which priorities are important or when evaluation criteria are subjective in nature.
The Paired Comparison Analysis also helps when potential options are competing with each other, because the most effective solution will be chosen in the end. It’s easier to set priorities when there are no conflicting requirements.
6 steps to apply the Paired Comparison Method
To apply Paired Comparison Method, it’s wise to use a large sheet of paper or a flip chart. Follow the steps below one by one for the analysis to work best.
Step 1: Creating table
Make a table with rows and columns and fill out the options that will be compared to one another in the first row and the first column (the headers of the rows and columns). The empty cells will stay empty for now. If there are 4 options, there are 4 rows and 4 columns and 16 cells; when there are 3 options, you get 3 rows and 3 columns and 9 cells, etcetera.
Step 2: Assigning letters
Every option is now assigned a letter (A, B, C etcetera). The options are mentioned in the headers of the rows and columns and each now has a letter so the options can be properly compared to each other.
Step 3: Blocking cells
It’s important to block out the cells in the table in which the same options overlap. Cells that contain a comparison that has been displayed earlier in the table also have to be blocked out. Every comparison should only be made once.
Step 4: Comparing options
The cells that are left will now compare the options in the rows to the options in the columns. The letter of the most important option will be noted. For example, when A is compared to C and C is a more important option, a C will be written down in that cell.
Step 5: Rating options
The difference in importance will now get a rating that will range, for example, from 0 (no difference) to 3 (important difference).
Step 6: Listing results
The results are now consolidated by adding all values for each of the options in question. If necessary, these totals can be converted to percentages.
Example of Paired Comparison Method
To clarify the way a Paired Comparison Method works, here is an example.
Take a commercial company that has to make a choice between three different Customer Relation Management (CRM) systems.
The first option is a CRM system by a renowned brand, the second option is a CRM system that is connected to a cloud service and the third option is a CRM system that consists of various modules. These options are assigned a letter and are put in the headers of rows and columns.
In step 3, a few cells are blocked and in this example, 4 cells remain open (see example).
Filling in the scores
The table is now ready to be filled in. We have chosen a scoring system of 0-3. Every option is compared, after which the winning option will become clear. A is compared to B, B to C, and C to A.
In the first comparison, A turns out to be more important than B, so the letter A is written down in the open cell. In the second comparison, C turns out to be more important than B, so the letter C is written down in the open cell. The last comparison is A to C, and A is also more important here. That means the letter A is written down in the open cell.
Now we look at importance. If A is a lot more important than B, we put a 3 after A. If A is hardly important compared to C, it will get a score of 1. Finally, option C is of medium importance compared to B and therefore scores a 2 (see example).
Evaluation of this Paired Comparison Method example
Now that all cells are filled out, we can look at the results. Firstly, all scores are added. See the image below.
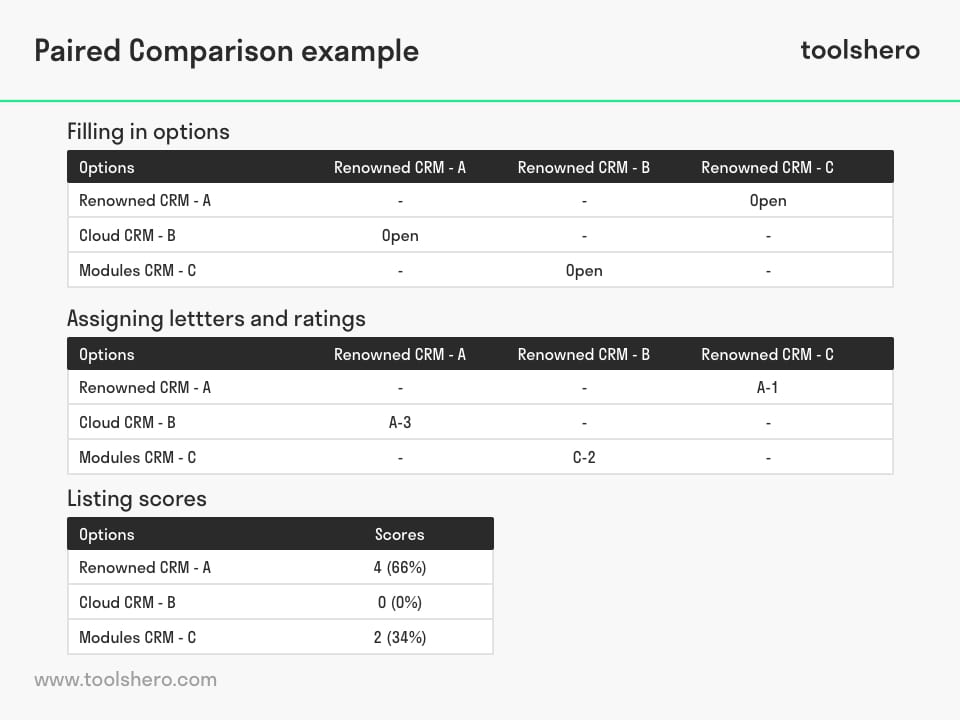
Figure 1 – Example of Paired Comparison Method
Option A – working with a renowned CRM system – is clearly the winner. The percentage is a simple calculation of the share of points compared to the total amount of points available.
The best option is instantly made clear by this analysis. We do need to take into consideration that this is a tool, and it shouldn’t be as the only way to make a decision.
If it turns out that working with the Modules CRM (C) gets is preferred by the majority in the company, that can certainly be the final decision.
It’s Your Turn
What do you think? Is the Paired Comparison Method applicable in your personal or professional environment? Do you recognize the practical explanation or do you have more suggestions? What are your success factors for good decision making?
Share your experience and knowledge in the comments box below.
More information
- David, H. A. (1963). The method of paired comparisons (Vol. 12). London.
- Silverstein, D. A., & Farrell, J. E. (2001). Efficient method for paired comparison. Journal of Electronic Imaging, 10(2), 394-399.
- Tarrow, S. (2010). The strategy of paired comparison: Toward a theory of practice. Comparative political studies, 43(2), 230-259.
How to cite this article:
Mulder, P. (2018). Paired Comparison Method. Retrieved [insert date] from Toolshero: https://www.toolshero.com/decision-making/paired-comparison-method/
Original publication date: 03/14/2018 | Last update: 09/19/2023
Add a link to this page on your website:
<a href=”https://www.toolshero.com/decision-making/paired-comparison-method/”>Toolshero: Paired Comparison Method</a>
Related ARTICLES
Borda Count Method: Basics and an Example
Stakeholder Analysis explained plus template
Prospect Theory by Amos Tversky and Daniel Kahneman
Convergent Thinking: the Definition and Theory
Decision Making Unit (DMU) explained
