Modern Portfolio Theory by Harry Markowitz
Modern Portfolio Theory (MPT): this article provides a practical explanation of the Modern Portfolio Theory (MPT) by Harry Markowitz. The article starts with a general definition of the Modern Portfolio Theory, followed by examples of basic formula and the steps involved to assess a portfolio. Then specific characteristics are explained and you will find some practical tips to use this model. Enjoy reading!
What is modern portfolio theory and investment analysis?
The Harry Markowitz’s Modern Portfolio Theory is an economic framework through which investors try to take minimal risks and maximize returns for a given investment portfolio.
This portfolio selection method emphasises that risk is inherent in a higher return, and that it is not enough to look at the expected risk and return of an individual asset.
By investing in more than a single asset, an investor can take better advantage of the benefits of diversification through a reduction in high-risk stocks.
The risk of individual shares is higher than the risk of shares in diversified portfolios, provided that the risks of those different shares are not directly related.
Therefore, consider the modern portfolio as a method that includes two types of high-risk stocks: one that yields profit when it rains, and the other that yields profit when it doesn’t. A portfolio that includes both types of shares will always bear fruit.
The Modern Portfolio Theory (MPT) was presented by economist Harry Markowitz in an essay from 1952. He was later awarded a Nobel Prize in Economics.
The relationship between risk and expected return
The Harry Markowitz’s Modern Portfolio Theory assumes that investors are risk-averse. This means that they prefer a portfolio with less risk over a risky portfolio with a certain level of return. An investor only takes more risk if the expected return is higher.
The expected return of a combined set of shares (the portfolio) is calculated as a weighted sum of the return on the individual shares. Suppose a portfolio consists of 5 stocks with an expected return of 3, 6, 9, 12, and 15%, then the sum for calculating the average expected return is:
Expected return = (3% x 20%) + (6% x 20%) + (9% x 20%) + (12% x 20%) + (15% x 20%)
Risk-reward ratio
The risk-reward ratio refers to the potential reward an investor can earn for every euro or dollar invested. Many investors use the risk-reward ratio to decide whether they can achieve their desired return with an investment.
An investment with a risk-reward ratio of 1:5 suggests that an investor is willing to invest 1 euro with the prospect of earning 5 euros. A risk-reward ratio of 1:3 indicates that an investor expects to earn 3 euros on his investment of 1 euro.
Trading uses this approach to plan the right transactions at the right time. The ratio is calculated by dividing the amount that may be lost as a result of an unexpected new price by the amount of profit that trading expects to make when the position closes.
When assessing the suitability of equities by investors, 1:3 expected return is often considered ideal. This means investors expect three units of return for each unit of additional risk. Investors use various tools to control the risk-reward ratio, such as stop-loss orders and put options.
A stop-loss order is a trading trigger that automates the sale of a stock from a given portfolio when the stock has hit a specific low. A put option is a contract that gives the investor the right to sell a specified amount of an underlying security at a predetermined price within a specified time frame.
Diversification in the investor portfolio
A popular adage in the investing world is ‘don’t put all your eggs in one basket’. In other words, investors advise against investing all capital in one company, index or other area. They advise this because the risk of losing all capital in the event of a crisis will be significant.
Instead, they advise looking at a variety of investments that vary when it comes to return and risk. This systematic risk spreading process is referred to as diversification and is the guiding principle behind the Modern Portfolio Theory (MPT). Several studies have shown that diversification can reduce portfolio risk by 25%.
Steps of Harry Markowitz’s Modern Portfolio Theory
Each investment has an impact on the return and risk of the entire portfolio. The first step in assessing this portfolio is to determine the expected value of the future return on the investment.
The second step is to focus on the fluctuation range of the return because investor developments may deviate from expectations. This involves analysing the standard deviation of the expected revenues. This helps determine outliers in both directions.
It is then necessary to determine whether there is a connection between investments. This is referred to as correlation. Correlation has a value between 1 and -1. If an investment does not respond to the fluctuation of another investment’s value, they do not correlate and the correlation value is equal to 0.
If a value fluctuation of one share does not always respond to the fluctuation of another share, the correlation is weak and closer to 0. Investments and fluctuations in value can also have a negative correlation. In that case, an increase in the value of one share leads to a lower value of another share.
Examples of positive and negative correlations between investments
An example of a positive correlation between shares or options is the price of crude oil and the shares of large oil companies. When the oil price rises, the shares of these oil companies will also rise.
If oil prices fall, the value of the oil company’s shares also decreases. This is because their sales and profit decline due to the lower selling price of a barrel of crude oil.
Another example is the price correlation between gold and silver. Both are precious metals, or alternative investment objects. The price of silver rises as the price of gold rises, and vice versa.
An example of a negative correlation between stocks or options is the relationship between national stock indices and the price of gold. When a national stock index rises, the gold price usually falls.
This is because gold is considered a safe haven for storing money. When the stock index rises, investors return to gold more often. They sell their shares in gold when traditional stocks are accelerating to take advantage of the upswing.
Characteristics of the Modern Portfolio Theory (MPT)
A portfolio of stocks that holds only positively correlated investments together ignores the fundamentals of diversification and is unlikely to withstand a crisis.
So if all investments are interrelated, they all fall simultaneously in worse times. The loss of a specific group of shares is therefore not compensated for by a group of shares that increases in value.
Investors generally try to balance the portfolio as much as possible. According to the creator of the Modern Portfolio Theory (MPT), an efficient portfolio is a series of investments that can achieve maximum returns at the lowest possible risk that the investors wants to and can take.
Groups of shares are placed in risk groups. A good portfolio consists of shares of several groups. A possible classification of these groups is as follows:
Risk group 1
These are stable and safe investment options. This group includes:
- Savings books
- European money market funds
- Cash
- Deposits with a fixed term
Risk group 2
These are conservative investment options. This group includes:
- Fixed-rate securities
- Bonds with high creditworthiness
- Pension funds
- Money market related funds
- Risk-free government bonds
Risk group 3
These are investment options that aim for solid profitability. This group includes:
- Shares of established companies
- Equity funds with default values
- International fixed income securities
- Shares and mixed funds
Risk group 4
This is a higher risk group with investment options that speculate on profit. This group includes:
- Shares and equity funds with default values
- Bonds with average ratings
- Bonds in foreign currency
- Investment funds
Risk group 5
This is the highest risk group with investment options with a lot of speculation. This group includes:
- Highly speculative bonds
- Loans
- Futures
- Junk bonds
- Other government bonds
According to the Modern Portfolio Theory (MPT), each risk group has its own efficient portfolio. These differ widely in composition, and are, as it were, a reflection of the investor’s risk tolerance.
On the one side of the spectrum are the highly speculative investment portfolios, and on the other the security-oriented portfolio. In between there are efficient portfolios with mixed investments.
Modern Portfolio Theory: efficient frontier
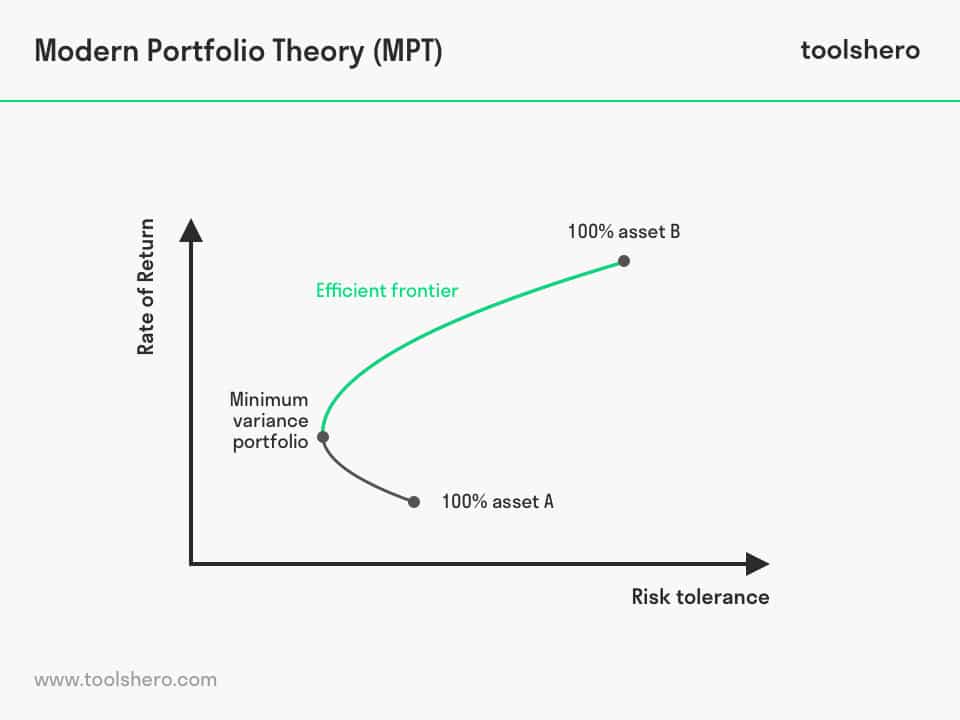
Figure 1 – Modern Portfolio Theory Example
The theory visualized this principle with a chart called the efficient frontier. The efficient frontier assesses portfolios on a return versus risk scale. The return is shown along the x axis and the associated risk along the y axis.
An investment portfolio within the efficient frontier is a set of optimal investment options that provide the highest expected return for a given level of risk. Portfolios that are below the efficient frontier are not optimal because they yield insufficient returns for the risk level attached to them. Portfolios clustered to the right of the efficient frontier are also not optimal because they have a higher level of risk for the expected return.
Like the Modern Portfolio Theory, the theory behind the Efficient Frontier was also introduced by Harry Markowitz, and is a cornerstone of the portfolio theory.
How is the efficient frontier established?
The efficient frontier graphically represents portfolios that maximise returns for an assumed risk. Returns depend on the investment combinations within a given portfolio. The standard deviation of an investment option is equal to the risk.
Ideally, the investor tries to fill his portfolio with options that offer exceptional returns, but whose combined standard deviation is less than the standard deviation of an individual option. If the mix of these options is ideal, the portfolio will be positioned along the efficient frontier line.
The curvature of the efficient frontier line is due to the diversification of investment options. The curvature shows how diversification improves the risk-return level of the portfolio. It also shows that there is a decreasing marginal risk.
The relationship between risk and reward is not linear. In other words, adding more risk to a particular portfolio will not yield the same return. Optimal portfolios generally have a higher degree of diversification than portfolios that are not optimal.
Harry Markowitz’s Modern Portfolio Theory summary
The Modern Portfolio Theory was introduced by Harry Markowitz and serves as a framework for investors to build an optimal investment portfolio.
The theory poses that risk and reward are inextricably linked, and that it is about a combination of shares with a higher risk/return and shares with a lower risk and return. Investors advise to include multiple investments in a particular portfolio that varies when it comes to return and risk. This risk spreading process is referred to as diversification and is the guiding principle behind the Modern Portfolio Theory (MPT).
It is then necessary to determine whether there is a connection between investments. This is referred to as correlation. Correlation has a value between 1 and -1.
An example of a positive correlation between shares or options is the price of crude oil and the shares of large oil companies. If the oil price rises, the value of these companies will increase and the shares will also increase in value. If a portfolio consists of an efficient combination of investment options, it will be on the efficient frontier. This is a graphical representation of a safe and modern investment portfolio.
More information
- Haugen, R. A., & Haugen, R. A. (2001). Modern investment theory (Vol. 5). Upper Saddle River, NJ: Prentice Hall.
- Markowitz, H. M. (1991). Foundations of portfolio theory. The journal of finance, 46(2), 469-477.
- Markowitz, H. M. (2010). Portfolio theory: as I still see it. Annu. Rev. Financ. Econ., 2(1), 1-23.
How to cite this article:
Janse, B. (2020). Modern Portfolio Theory (Markowitz). Retrieved [insert date] from Toolshero: https://www.toolshero.com/strategy/modern-portfolio-theory/
Original publication date: 03/14/2020 | Last update: 01/18/2024
Add a link to this page on your website:
<a href=”https://www.toolshero.com/strategy/modern-portfolio-theory/”>Toolshero: Modern Portfolio Theory (Markowitz)</a>
Ben Janse
Ben Janse is a young professional working at ToolsHero as Content Manager. He is also an International Business student at Rotterdam Business School where he focusses on analyzing and developing management models. Thanks to his theoretical and practical knowledge, he knows how to distinguish main- and side issues and to make the essence of each article clearly visible.
Related ARTICLES
Core Competence Model (Hamel and Prahalad)
PMESII-PT Analysis, an army Theory explained
Eight Dimensions of Quality by David Garvin
